[toc]

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

sort

关于时间复杂度：

  1. 平方阶 ($ O(n^2) $) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

  2. 线性对数阶 ($O(nlog_2(n))$) 排序 快速排序、堆排序和归并排序。

  3. ($O(n+§)$) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序。

  4. 线性阶 ($O(n)$) 排序 基数排序，此外还有桶、箱排序。

关于稳定性：

  1. 稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

  2. 不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

  • n：数据规模

  • k：“桶”的个数

  • In-place：占用常数内存，不占用额外内存

  • Out-place：占用额外内存

  • 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

1
2
import random
import time
1
2
3
4
5
6
7
8
9
10
11
12
def counter(sort):
    nums = []
    time_sum = 0
    for _ in range(1000):
        nums = []
        for i in range(100):
            nums.append(i)
        time_start = time.time()
        sort(nums)
        time_end = time.time()
        time_sum += (time_end - time_start)
    return time_sum

冒泡排序

冒泡排序算法的运作如下：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
以上节选自维基百科

1
2
3
4
5
6
7
8
9
10
11
def bubble_sort(nums):
    length = len(nums)
    for i in range(length):
        change_flag = False
        for j in range(1, length - i):
            if nums[j - 1] > nums[j]:
                change_flag = True
                nums[j], nums[j - 1] = nums[j - 1], nums[j]
        if change_flag == False:
            return nums
    return nums
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(bubble_sort(nums))
print(f"运行时间测试: {counter(bubble_sort)}(s)")
1
2
3
4
5
未排序数组：
[11, 5, 8, 12, 9, 6, 1, 19, 17, 3, 18, 4, 13, 10, 14, 2, 7, 0, 15, 16]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.00996851921081543(s)

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

以上节选自维基百科

1
2
3
4
5
6
7
8
9
10
11
def selectionSort(arr):
    for i in range(len(arr) - 1):
        # 记录最小数的索引
        minIndex = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[minIndex]:
                minIndex = j
        # i 不是最小数时，将 i 和最小数进行交换
        if i != minIndex:
            arr[i], arr[minIndex] = arr[minIndex], arr[i]
    return arr
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(selectionSort(nums))
print(f"运行时间测试: {counter(selectionSort)}(s)")
1
2
3
4
5
未排序数组：
[10, 13, 0, 18, 12, 2, 8, 17, 7, 16, 15, 11, 6, 3, 9, 5, 1, 19, 4, 14]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.4408740997314453(s)

插入排序

步骤如下

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤 2~5
以上节选自维基百科

1
2
3
4
5
6
7
8
9
def insertionSort(arr):
    for i in range(len(arr)):
        preIndex = i - 1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex + 1] = arr[preIndex]
            preIndex -= 1
        arr[preIndex + 1] = current
    return arr
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(insertionSort(nums))
print(f"运行时间测试: {counter(insertionSort)}(s)")
1
2
3
4
5
未排序数组：
[10, 15, 14, 7, 9, 8, 6, 3, 11, 16, 19, 18, 0, 4, 2, 17, 1, 12, 5, 13]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.024000167846679688(s)

希尔排序

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

以上节选自维基百科

1
2
3
4
5
6
7
8
9
10
11
12
13
def shell_sort(numberlist):
    length = len(numberlist)
    gap = length // 2
    while gap > 0:
        for i in range(gap, length):
            temp = numberlist[i]
            j = i
            while j >= gap and numberlist[j - gap] > temp:
                numberlist[j] = numberlist[j - gap]
                j -= gap
            numberlist[j] = temp
        gap = gap // 2
    return numberlist
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(shell_sort(nums))
print(f"运行时间测试: {counter(shell_sort)}(s)")
1
2
3
4
5
未排序数组：
[17, 9, 12, 18, 5, 14, 15, 2, 19, 13, 0, 16, 11, 6, 4, 7, 1, 8, 10, 3]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.11478352546691895(s)

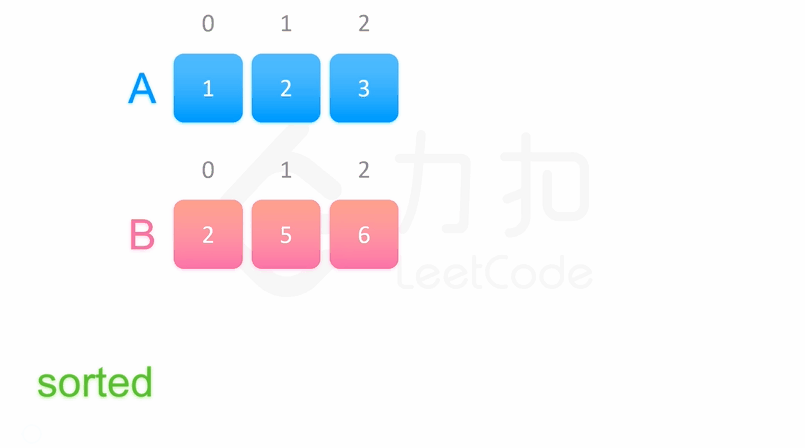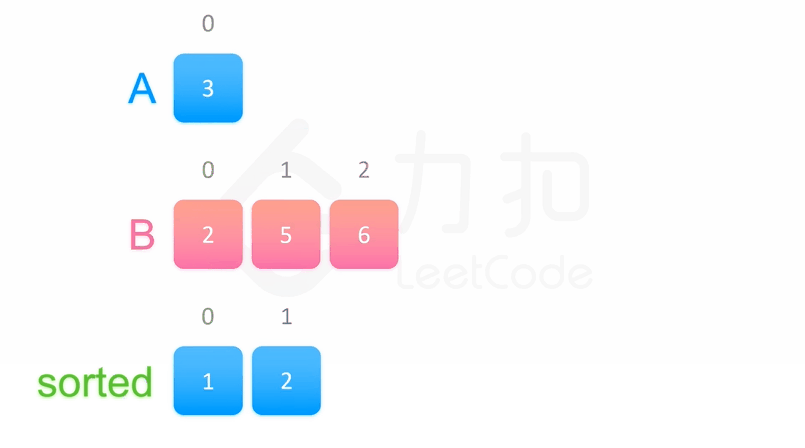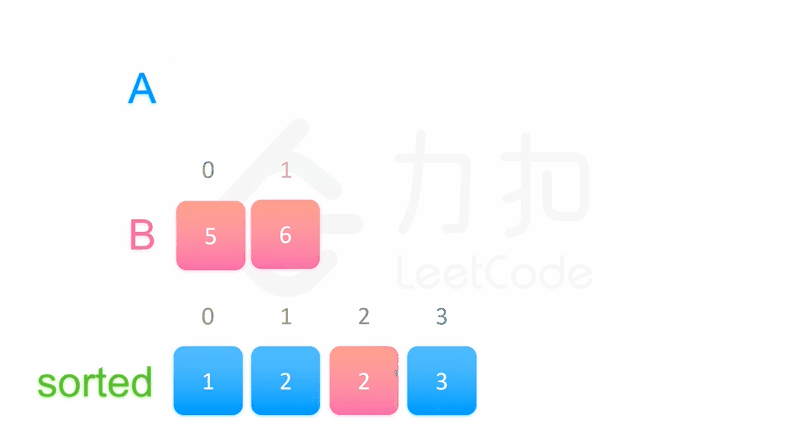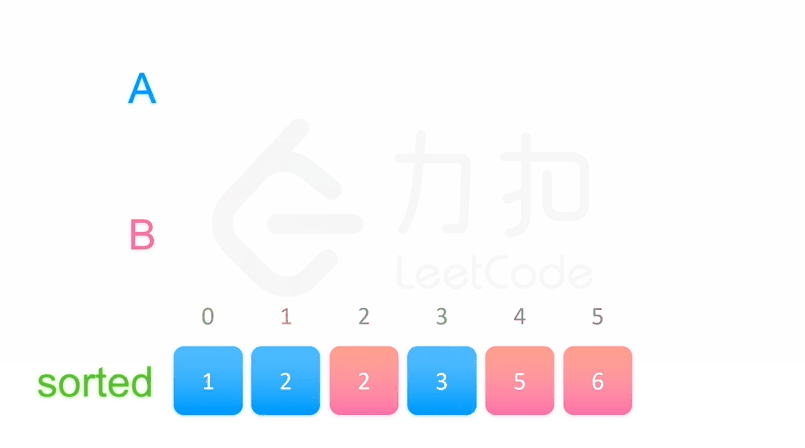
归并排序

原理如下（假设序列共有{displaystyle n}个元素）：

将序列每相邻两个数字进行归并操作，形成{displaystyle ceil(n/2)}个序列，排序后每个序列包含两/一个元素
若此时序列数不是 1 个则将上述序列再次归并，形成{displaystyle ceil(n/4)}个序列，每个序列包含四/三个元素
重复步骤 2，直到所有元素排序完毕，即序列数为 1
以上节选自维基百科

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def merge_sort(arr):
    if(len(arr) < 2):
        return arr
    middle = len(arr) // 2
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0));
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0));
    while right:
        result.append(right.pop(0));
    return result
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(merge_sort(nums))
print(f"运行时间测试: {counter(merge_sort)}(s)")
1
2
3
4
5
未排序数组：
[17, 0, 15, 18, 11, 5, 2, 1, 10, 9, 7, 19, 12, 6, 4, 3, 14, 13, 16, 8]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.2873060703277588(s)

快速排序

从数列中挑出一个元素，称为“基准”（pivot），
重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分割结束之后，该基准就处于数列的中间位置。这个称为分割（partition）操作。
递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

以上节选自维基百科

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def quick_sort(nums):
    def randomized_partition(nums, l, r):
        pivot = random.randint(l, r)
        nums[pivot], nums[r] = nums[r], nums[pivot]
        i = l - 1
        for j in range(l, r):
            if nums[j] < nums[r]:
                i += 1
                nums[j], nums[i] = nums[i], nums[j]
        i += 1
        nums[i], nums[r] = nums[r], nums[i]
        return i

    def randomized_quicksort(nums, l, r):
        if r - l <= 0:
            return
        mid = randomized_partition(nums, l, r)
        randomized_quicksort(nums, l, mid - 1)
        randomized_quicksort(nums, mid + 1, r)

    randomized_quicksort(nums, 0, len(nums) - 1)
    return nums
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(quick_sort(nums))
print(f"运行时间测试: {counter(quick_sort)}(s)")
1
2
3
4
5
未排序数组：
[13, 5, 14, 2, 19, 7, 11, 4, 3, 0, 12, 16, 8, 15, 1, 6, 10, 18, 9, 17]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.31716418266296387(s)

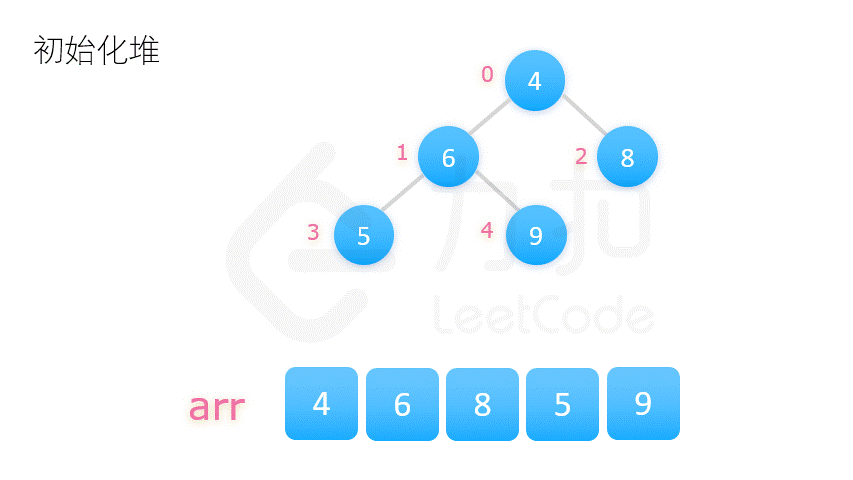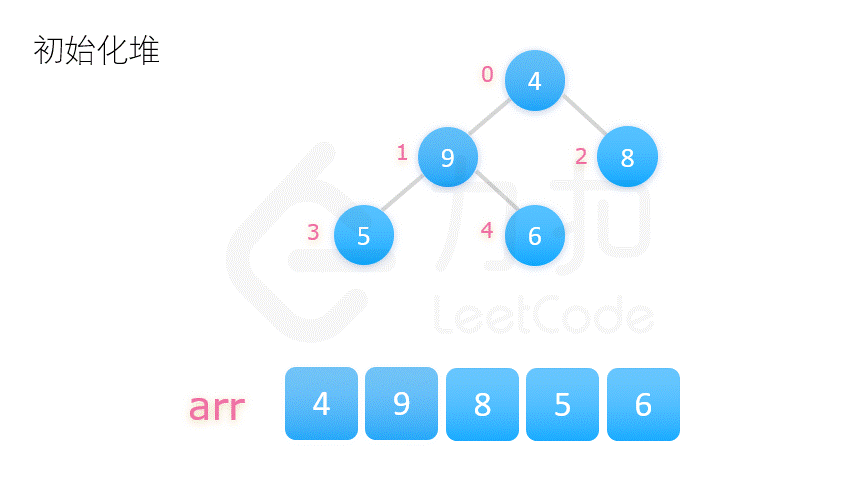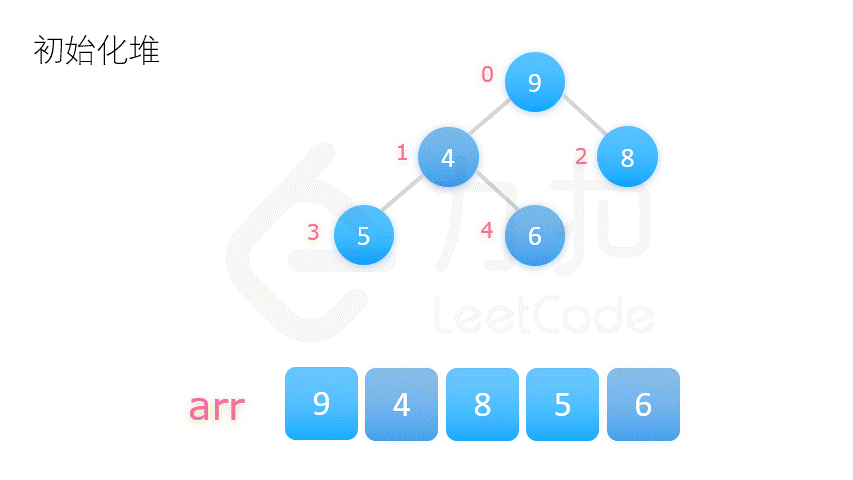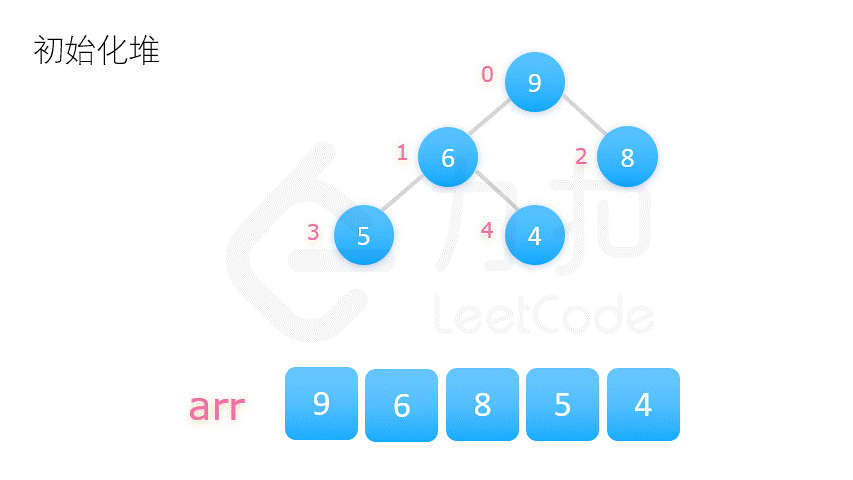
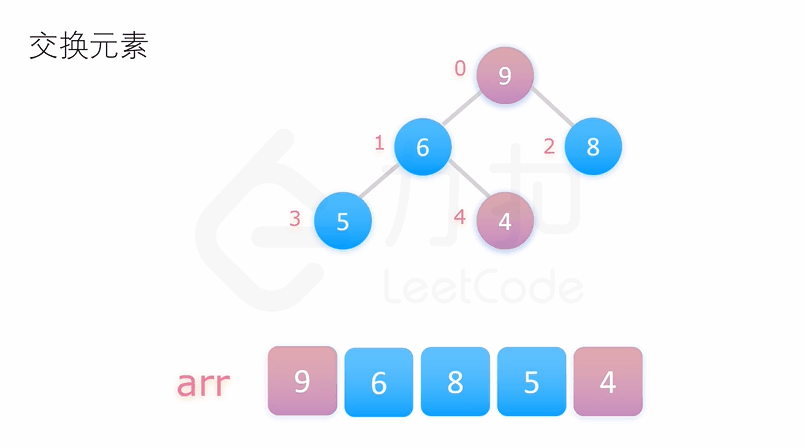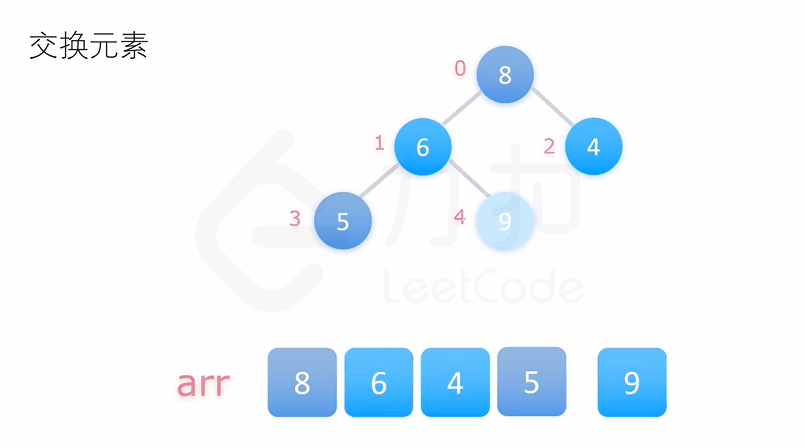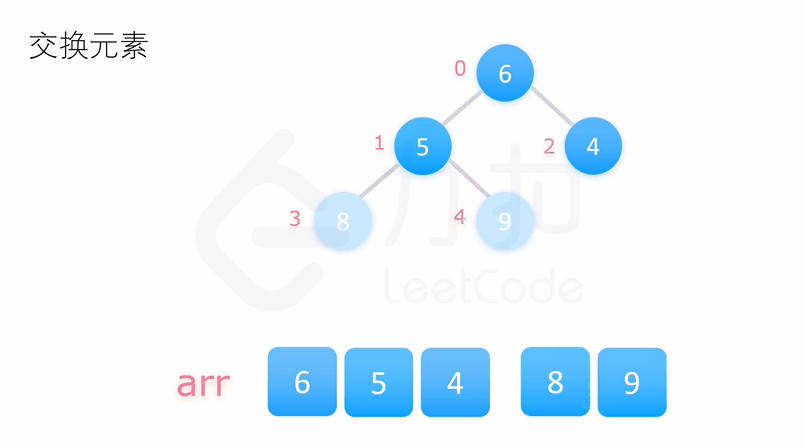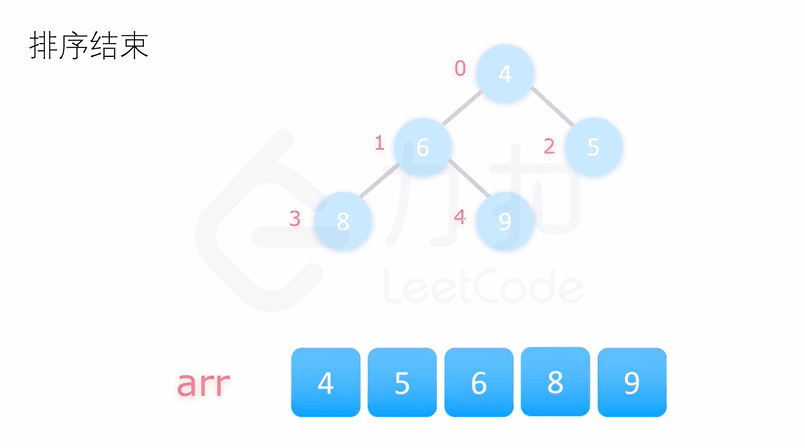
堆排序

若以升序排序说明，把数组转换成最大堆积(Max-Heap Heap)，这是一种满足最大堆积性质(Max-Heap Property)的二叉树：对于除了根之外的每个节点 i, A[parent(i)] ≥ A[i]。

重复从最大堆积取出数值最大的结点(把根结点和最后一个结点交换，把交换后的最后一个结点移出堆)，并让残余的堆积维持最大堆积性质。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def heap_sort(numberlist):
    # 下沉
    def sift_down(start, end):
        root = start
        while True:
            child = 2 * root + 1  # left child
            if child > end:
                break
            if child + 1 <= end and numberlist[child] < numberlist[child + 1]:  # has right_child && left_child.val < right_child.val
                child += 1  # change to right_child
            if numberlist[root] < numberlist[child]: # root.val < left child.val
                numberlist[root], numberlist[child] = numberlist[child], numberlist[root]
                root = child
            else:
                break

    length = len(numberlist)
    # 创建最大堆
    for start in range((length - 2) // 2, -1, -1):
        sift_down(start, length - 1)

    # 堆排序
    for end in range(length - 1, 0, -1):
        numberlist[0], numberlist[end] = numberlist[end], numberlist[0]
        sift_down(0, end - 1)

    return numberlist
1
2
3
4
5
6
7
8
9
10
nums = []
for i in range(20):
    nums.append(i)

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(heap_sort(nums))
print(f"运行时间测试: {counter(heap_sort)}(s)")
1
2
3
4
5
未排序数组：
[18, 2, 11, 1, 9, 10, 13, 8, 14, 7, 17, 6, 16, 4, 3, 5, 15, 12, 0, 19]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.4019196033477783(s)

python heapq

堆的定义：

堆是一种特殊的数据结构，它的通常的表示是它的根结点的值最大或者是最小。

python 中heapq的使用

列出一些常见的用法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
heap = [] # 建立一个常见的堆

heappush(heap,item) # 往堆中插入一条新的值

item = heappop(heap) # 弹出最小的值

item = heap[0] # 查看堆中最小的值，不弹出

heapify(x) # 以线性时间将一个列表转为堆

item = heapreplace(heap,item) # 弹出一个最小的值，然后将item插入到堆当中。堆的整体的结构不会发生改变。
heappoppush() # 弹出最小的值，并且将新的值插入其中

merge() # 将多个堆进行合并

nlargest(n , iterbale, key=None) # 从堆中找出做大的N个数，key的作用和sorted( )方法里面的key类似，用列表元素的某个属性和函数作为关键字
1
2
3
4
5
6
7
8
# 使用python内置库
from heapq import *

def heapsort(iterable):
    h = []
    for value in iterable:
        heappush(h, value)
    return [heappop(h) for i in range(len(h))]

计数排序

以上节选自维基百科
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def counting_sort(input_list):
    length = len(input_list)

    if length < 2:
        return input_list

    max_num = max(input_list)
    count = [0] * (max_num + 1)  # 多加一个0
    for element in input_list:
        count[element] += 1

    output_list = []
    for i in range(max_num + 1):
        for j in range(count[i]):  # count[i]表示元素i出现的次数，如果有多次，通过循环重复追加
            output_list.append(i)
    return output_list
1
2
3
4
5
6
7
8
9
10
11
12
nums = []
for i in range(20):
    nums.append(i)

# nums = [16, 16, 16, 16, 10, 4, 8, 2, 12, 14, 13, 17, 15, 7, 0, 3, 1, 5, 6, 9]

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(counting_sort(nums))
print(f"运行时间测试: {counter(counting_sort)}(s)")
1
2
3
4
5
未排序数组：
[6, 19, 5, 7, 17, 0, 12, 9, 3, 15, 18, 13, 14, 10, 11, 1, 2, 16, 8, 4]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.039923667907714844(s)

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

在额外空间充足的情况下，尽量增大桶的数量

使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

（1）什么时候最快

当输入的数据可以均匀的分配到每一个桶中。

（2）什么时候最慢

当输入的数据被分配到了同一个桶中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def bucket_sort(s):
    """桶排序"""
    min_num = min(s)
    max_num = max(s)
    # 桶的大小
    bucket_range = (max_num - min_num) / len(s)
    # 桶数组
    count_list = [ [] for i in range(len(s) + 1)]
    # 向桶数组填数
    for i in s:
        count_list[int((i-min_num) // bucket_range)].append(i)
    s.clear()
    # 回填，这里桶内部排序直接调用了sorted
    for i in count_list:
        for j in sorted(i):
            s.append(j)
1
2
3
4
5
6
7
8
9
10
11
12
nums = []
for i in range(20):
    nums.append(i)

# nums = [16, 16, 16, 16, 10, 4, 8, 2, 12, 14, 13, 17, 15, 7, 0, 3, 1, 5, 6, 9]

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(bucket_sort(nums))
print(f"运行时间测试: {counter(bucket_sort)}(s)")
1
2
3
4
5
未排序数组：
[17, 6, 3, 19, 11, 12, 15, 9, 4, 0, 16, 18, 14, 8, 13, 7, 1, 10, 5, 2]
排序后数组：
None
运行时间测试: 0.05981326103210449(s)

基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

  • 基数排序：根据键值的每位数字来分配桶；

  • 计数排序：每个桶只存储单一键值；

  • 桶排序：每个桶存储一定范围的数值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def radix_sort(list):
    i = 0                                    #初始为个位排序
    n = 1                                     #最小的位数置为1（包含0）
    max_num = max(list) #得到带排序数组中最大数
    while max_num > 10**n: #得到最大数是几位数
        n += 1
    while i < n:
        bucket = {} #用字典构建桶
        for x in range(10):
            bucket.setdefault(x, []) #将每个桶置空
        for x in list: #对每一位进行排序
            radix =int((x / (10**i)) % 10) #得到每位的基数
            bucket[radix].append(x) #将对应的数组元素加入到相 #应位基数的桶中
        j = 0
        for k in range(10):
            if len(bucket[k]) != 0: #若桶不为空
                for y in bucket[k]: #将该桶中每个元素
                    list[j] = y #放回到数组中
                    j += 1
        i += 1
    return  list
1
2
3
4
5
6
7
8
9
10
11
12
nums = []
for i in range(20):
    nums.append(i)

# nums = [16, 16, 16, 16, 10, 4, 8, 2, 12, 14, 13, 17, 15, 7, 0, 3, 1, 5, 6, 9]

random.shuffle(nums)  # 打乱数组nums的顺序
print("未排序数组：")
print(nums)
print("排序后数组：")
print(radix_sort(nums))
print(f"运行时间测试: {counter(radix_sort)}(s)")
1
2
3
4
5
未排序数组：
[11, 4, 9, 7, 2, 13, 15, 5, 19, 10, 1, 18, 16, 17, 6, 3, 0, 8, 14, 12]
排序后数组：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
运行时间测试: 0.09178805351257324(s)